C какой хитрой задачкой сталкивались абитуриенты Гарварда в XIX веке
- 15 августа 2018 09:45
- masterok.livejournal.com
Пишут, что такую задачку задавали на вступительных экзаменах в Гарварде в 1869 году. В интернете часто встречаются подобные, да еще со всякими подвохами. Мне они всегда тяжело давались, что-то математическая тренировка у меня уже не та.
А эта задачка показалась мне совсем нетрудной в решении. Тут не нужно использовать какие-то хитрые рассуждения и математические подходы.
Если правильно понять направление решения — все идет очень легко. Все, конечно, ринулись решать с помощью системы уравнений — а попробуйте без них.
Вот как звучит задачка:
Мужчина купил наручные часы, цепочку и медальон за 216 долларов. Часы и медальон в совокупности стоят втрое больше, чем цепочка. Цена цепочки и медальона в совокупности вдвое ниже, чем цена часов. Назовите цену каждого предмета по отдельности.
Попробуйте вычислить, какому числу равен каждый символ. Подумайте сначала самостоятельно, а под катом я вам покажу решение и правильный ответ.
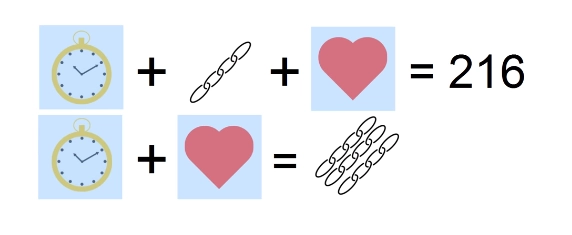
Перерисуем условие еще раз, преобразовав третье условие для удобства решения:
Обратите внимание на вот эту конструкцию:
Ничего не замечаете?
Ну конечно же, логично сделать такой вывод…
Отсюда сразу же имеем…
Так, один символ разгадали. Его числовое значение получили.
Теперь разберемся с вот этой ситуацией:
или
или
Видим, что часы — это 162 минус «сердце». Тогда получается, что если к третьей строке прибавить «сердце», то равно это будет как раз 162.
Ну и тут уже совсем просто:
и
Вот и второй символ рассчитали.
ИТОГО:
Как вам показалась эта задачка? Хитрых подвохов никаких нет. Все решается прямой логикой и простейшими арифметическими приемами.
- Телеграм
- Дзен
- Подписывайтесь на наши каналы и первыми узнавайте о главных новостях и важнейших событиях дня.



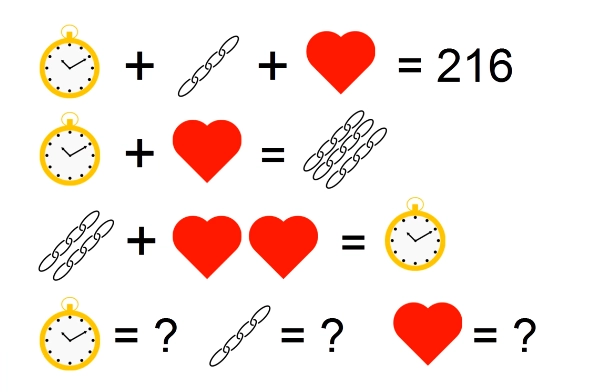
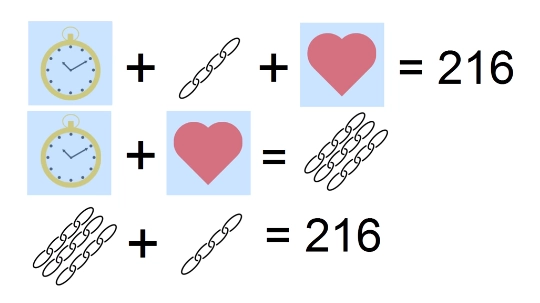
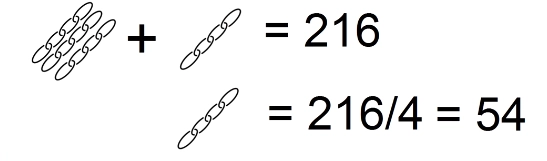
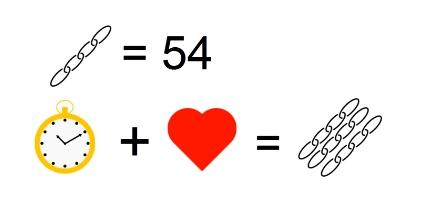
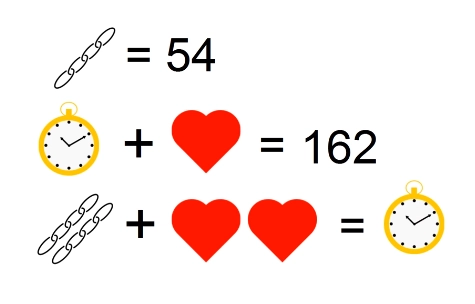
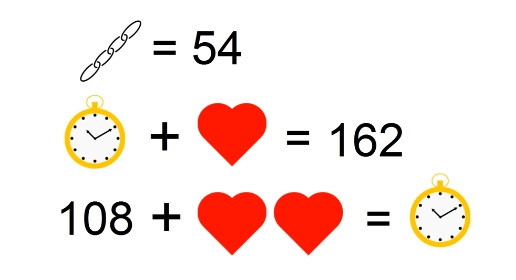


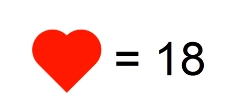
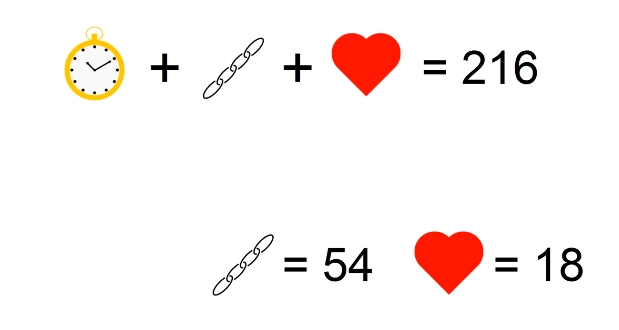
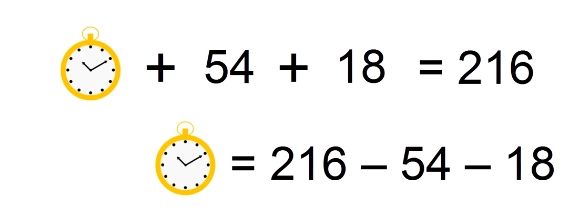
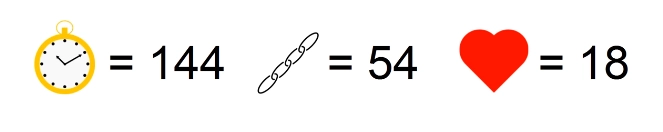
Войти через социальные сети: